Így neveld a laposföldesedet! – kalandozás egy összeesküvés-elmélet világában

Ha a cím valami lekezelőt sejtet, az csak reklámfogás. Valójában pont a lekezelés ellen fogok kiállni, valamint egy laza ismeretelméleti terepsétára hívom az olvasót.

A természettudomány látványosan hatástalan szerszámnak bizonyul, amikor ideológiai furkósbotként kezdjük lóbálni. Márpedig szerintem pont ez történik legtöbbször, mikor a laposföldmodell híveinek egyre növekvő táborával szembesülve a hagyományos gömbföldes (jó, tudom, geoid) modell mellett kiálló kommentátorok, influenszerek reagálnak a világnézetüket felborzoló „lapsi” tartalmakra. Arckaparásnál, egymás közötti szörnyülködésnél, felkészületlen kioktatási kísérleteknél vagy lemondó nagyazistenállatkertjézésnél kevesen jutnak tovább.

Paradox módon ilyenkor az történik, hogy a mi viselkedésünk válik dogmatizmussá. Hiszen lássuk be: kevesen figyeltünk már meg horizont mögött eltűnő hajót, kevesen méregettük távoli hegyek látszólagos magasságát, vagy bámultuk a Földet űrhajóból. A legtöbben a föld gömbölyű (geoid) voltát egyszerűen csak elhittük másoknak gyerekkorunkban, és megszoktuk a gondolatot – ez a kognitív bizalom nem hiba, viszont egy laposföldes pont ezt a bizalmat vesztette el a rendszerrel szemben.

Ezzel ellentétben a laposföldes gondolkodás (ha most leválasztjuk róla az életszerűtlen összeesküvés-elméleteket) bizony megvalósít valamit a természettudomány eredeti étoszából: semmit nem akar bemondásra elhinni a rendszernek, és kizárólag saját tapasztalatra szeretne hagyatkozni, mert elvileg már csak abban bízik. (Más kérdés, hogy egymásnak valószínűleg sok mindent elhisznek bemondásra, de ez nem a mi dolgunk.)

A bizalom nem racionális kérdés. Ha valaki elvesztette a bizalmát a tudományos, gazdasági, politikai rendszerben, mert nem sikerült jól szétszálaznia egymástól a bizalomra és kritikára okot adó rendszerrészeket, annak meggyőzésére – ha ez egyáltalán lehetséges – csak az ő saját játékszabályai szerint van már esélyünk. De így is működhet a tudomány! Mert a tudományos módszert nem, hanem csak az intézményt tagadják meg a laposföldesek, amikor visszahelyezkednek egy fundamentalista empirizmusba.

Állítom: egy laposföldest nekünk, gömbföldeseknek a saját észjárása keretei között kell felkeresnünk, és az ő paradigmájában is releváns ellenérveket kell keresnünk a laposföld-felfogás ellen.

Pepecs munka lehet, és alázatot kíván, de érdemes megpróbálni: még ha neki már mindegy is, a közönség miatt, amely a közösségi média révén mindig ott figyel a háttérben, és ahonnan új és új tudománytagadók toborzódnak, mindenképpen érdemes. Tudósként fellépni pedig konyhai körülmények között is lehet. Egy kis kutatás és számolgatás erejéig valami ilyesmire tettem kísérletet, és megpróbáltam laposföldes térfélen nyerni egy elméleti csörtét gömbföldesként. Nézzük, mire jutottam!

Egy laposföld-érv

A 200 bizonyíték arra, hogy a Föld nem egy forgó gömb című, Eric Dubay által jegyzett érvgyűjtemény a laposföldes közösség egyik bibliája. Ebben a 39. számú érv (a gyűjtemény sok más, sajnos kimondottan hitvány érvével ellentétben) történetesen egy jó érv, mivel kielégíti a tudományosság néhány fontos kritériumát: ellenőrizhető tényállításokat tartalmaz, fogalmi következtetése világos és logikailag helyes, és az, hogy igaz-e vagy sem, a gömb- és laposföld-modellek közötti választás szempontjából valóban mérvadó. Így hangzik (és csak első olvasatra tűnhet bonyolultnak, valójában nem az, mindjárt el is magyarázom):

"39) A »The Australian Handbook, Almanack, Shippers’ and Importers’ Directory« (Ausztrál Kézikönyv és Almanach – Hajós fuvarozók és importőrök jegyzéke) című könyvben található gyakorlati távolsági mérések alapján a Sydney-t és Nelsont összekötő egyenes vonal mentén a távolság 1550 mérföld (kb. 2500 km). A hosszúsági fokaik közti eltérés 22 fok, 2’14”. Ezért, ha 360 fokból 22 fok 2’14” 1550 mérföldnek (kb. 2500 km) felel meg, akkor az egész Földnél ez 25 182 mérföldet (kb. 40 500 km) jelentene. Ez nagyobb az állítólagos gömbföld Egyenlítő mentén mérhető kerületénél is, és 4262 mérfölddel (kb. 6860 km) hosszabb, mint a Sydney-nél található déli szélességi kör mérete lenne a gömbföldön az említett arányok mellett."

Itt fontos az Almanachra történő hivatkozás. Joggal gondolhatjuk, hogy ez a kiadvány olyanok szerkesztésében és olyanoknak készülhetett, akiknek gyakorlati érdekük volt, hogy valós távolságadatokkal dolgozzanak, mégpedig valódi hajósok valódi távolságmérései alapján. Nem hihető tehát, hogy engedték volna, hogy egy esetleg nem létező gömbföldről hazudozó háttérmanipuláció valahogy meghamisítsa az adatközlésüket. Egy laposföld-hívő szemében ez tehát megbízható forrásnak tűnhet, és láthatjuk, hogy a laposföldes Eric Dubaynak is hivatkozási alap: ha nem is saját, de azért megbízható tapasztalat.

Az pedig tény, hogy két eltérő hosszúsági körön fekvő helyszín kelet–nyugati irányú távolságából és hosszúsági köreik szögeltéréséből egyszerűen kiszámolható a teljes szélességi körük hossza. A számítás csupán annyi, hogy a kelet–nyugati távolságot meg kell szorozni annyival, ahányszor nagyobb a teljes 360 fok a két hely hosszúsági köreinek szögeltérésénél (vagyis 22° 2’14”-nél azaz 22,037°-nál, de az egyszerűség kedvéért vegyük ezt kereken 22°-nak), és máris kész a szélességi kör hossza:

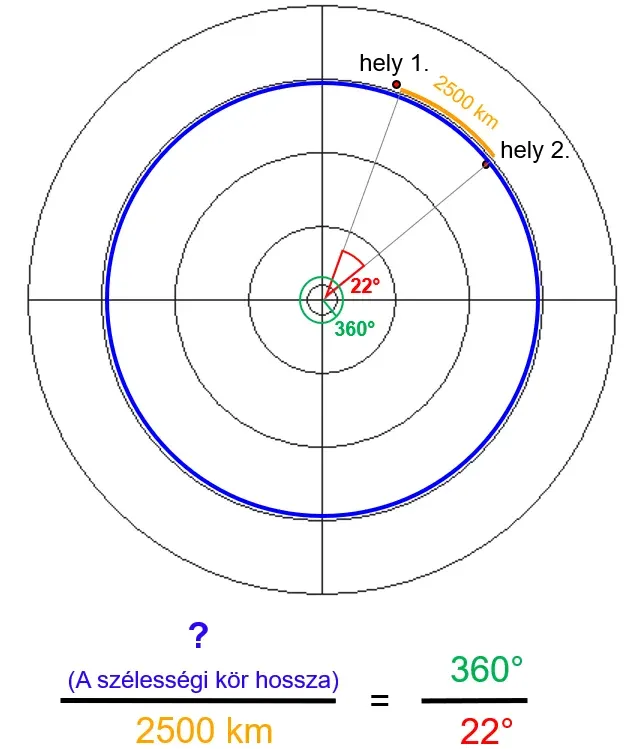
A tőlünk nézve Egyenlítőn túli (tudatosan kerülöm most a "déli" kifejezést) szélességi köröknek lapos Föld esetén hosszabbnak kellene lenniük, mint az Egyenlítő, hiszen a korong “kifelé” egyenletesen szélesedik; ezzel szemben gömbföld esetén rövidebbnek, hiszen ez esetben arrafelé már "szűkül" a földkerület a Déli-sark felé.

Ha tehát az Egyenlítő túloldalán lévő, ausztráliai Sydney és az új-zélandi Nelson kelet–nyugati irányú távolságát tényleg 2500 kilométernek mérik a hajósok, de elfogadjuk a helyek földrajzi koordinátáit hitelesnek, ahogy azt Dubay logikája megengedi, akkor valóban körülbelül 40 909 kilométer jön ki nekünk is (360÷22×2500), ami még nagyobb is, mint Dubay eredménye – jóhiszeműen vélelmezhetjük, hogy számításakor korrigálta a földrajzi szélességek kis különbségéből fakadó "átlósságot", és csak az útvonal kelet–nyugati irányú vetületével számolt.

Mindenesetre tényleg nagyobb szám jön ki az Egyenlítő 40 075 kilométeres hosszánál, ami a gömbföldmodellel valóban nem összeegyeztethető.

Igen ám, de alapelvünk, hogy nem fogadunk el semmit bemondásra, így hát Dubaynak az Almanach távolságközléséről szóló közlésében sem bízhatunk vakon. Ha valaki nem tudja vagy nem akarja személyesen csekkolni az adatot a hivatkozott műben (ami lássuk be, nem is hangzik bárki által triviálisan elvégezhető kutatómunkának), akkor is van lehetősége hasonló, egyszerű és végső soron tapasztalati valóság-ellenőrzést végezni. Lássuk, hogyan!

A kutatás

Dél-Ausztráliában húzódik egy igen hosszú, kelet–nyugati irányú autóút, az Eyre Highway. Eszembe jutott, hogy alighanem vannak az út mentén távolságjelző táblák, melyek adatait tekinthetjük rendszerfüggetlenül hitelesnek, hiszen a helyiek bizonyára nem tűrnék el, ha a NASA suttyomban kihelyezett manipulációs objektumaiként rendszeresen dezinformálnák őket a megteendő távolságokról.

Ezekben a táblákban az a jó, hogy a Google Utcakép segítségével mi is könnyedén szemügyre vehetjük őket, de aki ebben az eszközben szigorú laposföldesként nem bízik, annak sincs szüksége különleges eszközre vagy szakképesítésre, hogy meggyőződjék valódiságukról. "Mindössze" el kell utazni Ausztráliába, felkeresni a táblákat, és megnézni, csakugyan ott vannak-e. Ha pedig nem, hát keresni kell a helyszínen más táblákat, és dolgozni azokkal. Áthidaló megoldás: megbízható ismerős Ausztráliából küldhet nekünk fotót koordinátákkal. Én, bevallom, megelégedtem a Utcaképpel, és a Google Földön kis keresgéléssel találtam is táblát!

Az Eyre Highway mentén fekvő apró település Eucla, mely egy 2021-es cenzus szerinti kemény 37 fős lélekszáma ellenére fontos megállóhely lehet a kietlen úton, mert igényes, információgazdag távolságjelző táblája van. A táblán feltüntetett távolságok kilométerben értendők, tekintve, hogy Ausztrália 1974 óta metrikus rendszert használ:

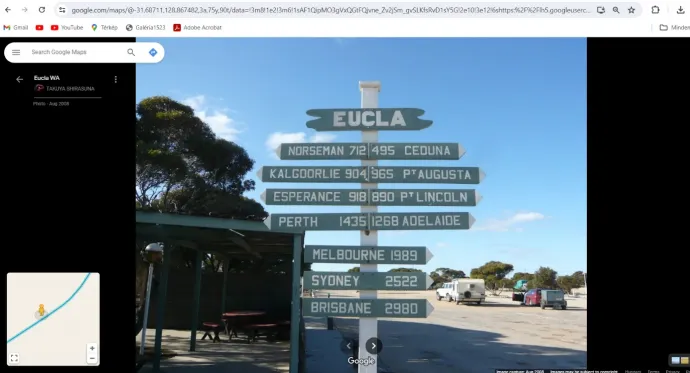
Fordított képkereséssel meggyőződtem róla, hogy a szemrevaló tábláról számos, különböző minőségű és korú fényképfelvétel kering a neten különböző rendű és rangú oldalakon, különböző szerzőktől, ami számomra elégségesen megnyugtató biztosítéka annak, hogy nem a Google által elém vetített káprázatról van szó. Ha ez a tábla tényleg ott van Euclában (amit, ismét aláhúzom, bárki személyesen ellenőrizhet Ausztráliába utazva), és hitelesek a rajta szereplő számok (amit az ellenkező esetben méltán várható népharag biztosít, de ha már úgyis ott járunk, le is autózhatjuk a távokat ellenőrzésképpen), úgy alighanem valós adatokhoz jutottunk konkrét helyek Euclától mérhető távolságáról. Közúton. Jöhet az elméleti munka!

Azért, hogy kellően nagy számokkal dolgozhassak, és ezzel a hibaarányt csökkentsem, a 2522 kilométeres Eucla–Sydney távolságot választottam a tábláról. Meg azért is, mert igen közeli szélességi körökön fekszik a két település (közelebbin is, mint Sydney és Nelson), így egyszerűen a kelet–nyugati távolságukkal számolhatok. Ha kérünk egy útvonaltervezést a Google Térképtől Euclától Sydney-be, 2504 kilométeres javaslatot kapunk mint legrövidebbet, ami elég jó egyezés a táblával (és bár ez önmagában is elég jól hitelesíti a Google rendszerének valósághűségét és ezzel a gömbföldmodellt, ezt nem fogom felhasználni érvként). Következő lépésként megmértem az alkalmazás segítségével a kelet–nyugati távolságot Eucla és Sydney között légvonalban, ami csak 2090 kilométerre jött ki, és ez hihetőnek is tűnik, tekintve, hogy levágtuk a sok kanyart, amelyeket az autóút megtesz:

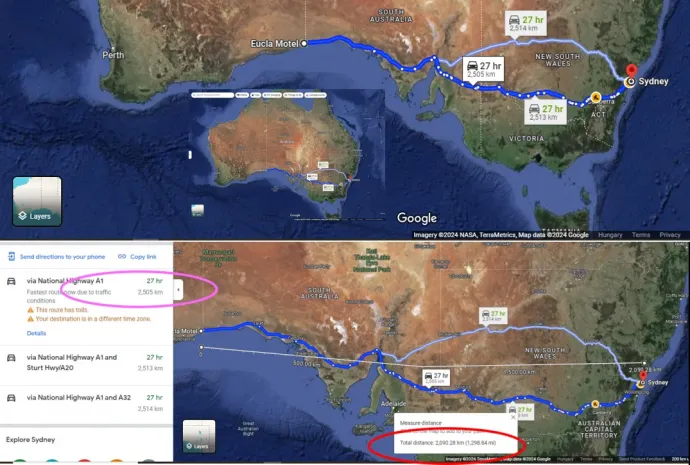
Van tehát légvonalam, mintha hajón mehetnék. Éberségem azonban nem lankadt, hiszen nyilván mindenre gyanakvó laposföldesek is górcső alá vehetik munkámat: ugyanezzel a módszerrel ellenőrzésképpen végigléptettem a távolságmérőt az autóút vonalán, és így már 2404 kilométert kaptam, ami meggyőzött arról, hogy végletesen aprólékos útvonalkövetéssel elérném a táblának is megfelelő 2500 kilométer körüli becslést. A Google-alkalmazásban végzett távolságbecslések tehát valószerűek, és így a légvonalas mérésem megbízhatatlanságára sem kell gyanakodnom. Bárki tetszőleges aprólékossággal, szabadon tovább pontosíthatja ellenőrző közelítésemet:

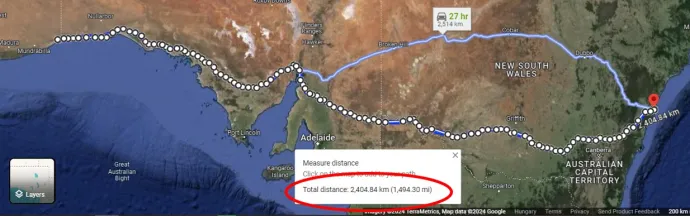
Számoljunk tehát a 2090 kilométeres légvonalbeli kelet–nyugati távolsággal Dubay módszerének megfelelően. Kellenek még a két hely földrajzi koordinátái. Ezeket a Google alkalmazásából másoltam ki, de hitelességüket ellenőriztem a két helység Wikipédia-oldalán és egy nyomtatott atlaszban is, és mindkettő szerint stimmelnek:

• Eucla: szélesség: -31,677326563450617° (déli), hosszúság: 128,88423424784617° (keleti)
• Sydney: szélesség: -33,820425865798654° (déli), hosszúság: 151,06238144735795° (keleti)

A hosszúsági fokok különbsége tehát kerekítve 22,18°. (A két szélességi kör számainak átlagolásával nyert közepes, vagyis közelítéssel “közös” szélességi kör: -32,75°, déli.)

Alkalmazva Dubay fent vázolt módszerét (vagyis a kelet–nyugati távolságot szorozva a teljes kör és a hosszúsági szögeltérés arányával) azt kapjuk, hogy az egyszerűség kedvéért itt közösnek tekintett szélességi kör hossza: 360÷22,18×2090, azaz 33 922,5 kilométer.

Ez bizony rövidebb, mint az Egyenlítő, ráadásul egész jól megegyezik az egyenlítő hosszából gömbföld esetén számolható elméleti értékkel, amely cos(32,75°) × 40 075, azaz 33 704 kilométer.

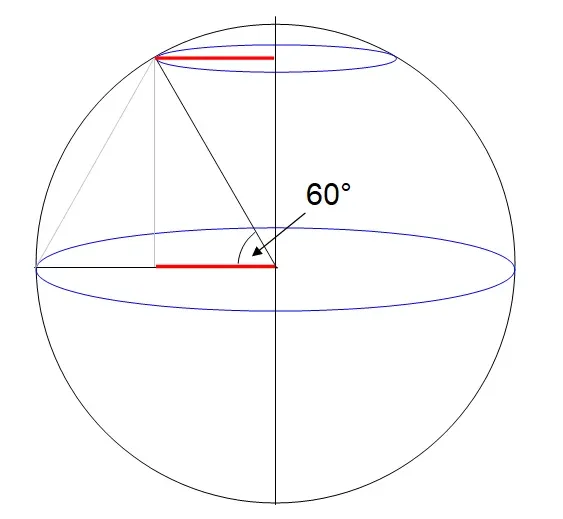
Utóbbi számítás magyarázata annak, akit érdekel: bármely gömbön egy szélességi kör hosszát megkapjuk, ha a főkör (Egyenlítő) hosszát megszorozzuk a szélességi kör fokszámának koszinuszával. Így például a 60. szélességi kör hossza fele az Egyenlítőének, mert cos(60°)=0,5. Ezt középsulis matektudással és egy kis rajzolgatással bárki beláthatja, ha észbe veszi, hogy egy fele akkora sugarú kör kerülete is feleakkora (2rπ helyett 1rπ).

A kis felkerekítéssel 33 900 kilométer hosszú Eucla–Sydney szélességi kör tehát rövidebb, mint a 40 074 km-es Egyenlítő, ami gömbföld esetén érthető, laposföld esetén azonban nem, mert ott az Egyenlítőnek megfelelő vonalon túli (gömbös szemléletben déli) szélességi köröknek hosszabbaknak kellene lenniük, mint az Egyenlítő. De ezek szerint nem azok. Dubay módszerével és független adatokból ily módon az övével ellentétes eredményre jutottunk a Sydney-közeli szélességi körök hosszával kapcsolatban. Sikerült tehát a laposföldes Eric Dubay hitelesítette gondolatmenettel, ausztráliai tapasztalati távolságok felhasználásával megerősítenünk a gömbföldmodellt, és gyengítenünk a laposföld-modell érvényességét.

Epilógus

Hab a tortán, hogy mindennek végeztével az esélytelenek nyugalmával bemásoltam a keresőbe, hogy “The Australian Handbook, Almanack, Shippers’ and Importers’ Directory”, és magam is meglepődtem, milyen hamar ráakadtam a National Library of Australia honlapján a mű eredeti példányokból fotózott, ugyanakkor szövegesen mégis profin kereshető példányaira, amelyeket bármiféle regisztráció nélkül szabadon tanulmányozhattam, ahogy megteheti ezek szerint bárki más is. 1873-tól 1880-ig nyolc kiadás is megtekinthető, és kis keresgéléssel sikerült is ráakadni mindegyikben Nelson városának ismertetésére, ahol valóban fel is tüntetik a távolságát a térség más nagyvárosaitól, így Sydney-től is:

Mind a nyolc évben minden példány következetesen 1180 mérföldet (azaz tengeri mérfölddel számolva 2185 kilométert) jelöl meg a két város távolságaként, ami erős jóindulattal sem kerekíthető a Dubay által közölt 1550 mérföldes értékre, és ha így végezzük el Dubay számítását, úgy már 35 760 kilométer hosszú szélességi kört kapunk Sydney környékére, ami rövidebb, mint az Egyenlítő, és elég jól egyezik az általunk (Eucla–Sydney alapon) számítottal. (Az hogy valamivel nagyobb, abból fakadhat, hogy a fokhálózaton nézve kissé átlós útvonal hosszúságát nem korrigáltam az észak–déli kitéréssel – akinek kedve van, tegye meg –, hanem egyből kelet–nyugatinak vettem az egészet.)

Ráadásul a Google Térkép kézi távolságmérésével is 2144 kilométert, visszaszámolva 1158 tengeri mérföldet kaptam a két város távolságára (ha belevettem a szükséges kanyart is a Tasman-öbölnél Nelson közelében, melyet a hajóknak muszáj bevenniük). Ez nagyon szép, több mint 98 százalékos egyezés a száznegyven éves hajózási adattal.

A forráskritika alapján tehát arra kell következtetnem, hogy Eric Dubay sajnos egyszerűen téves adatot közöl 39. számú érvében a két város Almanachból kiolvasható távolságára, és csak emiatt tűnik működőképesnek az érve.

A tanulság az, hogy miközben laposföldes módszerrel, laposföldes irányelvek mentén sikerült megerősíteni a gömbföldmodellt, addig a laposföldeseknek valamiben továbbra is igazuk van: nem esik le az aranygyűrű az ujjunkról, ha nekilátunk az aprómunkának, és időnként amennyire tudjuk, első kézből származó tapasztalatokra támaszkodva ellenőrizzük, amit tudni vélünk. Pláne, ha kételyekkel szembesülünk. Jó munkát mindenkinek!

A szerző a Veres Pálné Gimnázium biológia-természettudomány tanára.