Matekfelvételik: egy félreérthető kérdést rendbe rakott az Oktatási Hivatal, a másiknál azonban nem tágít

A vitatható pontot nem kapták meg a gyerekek, de akadt, akit az vigasztalt, hogy ő úgyis a legjobb matekosokkal versenyez a felvételi helyekért. Ők pedig – legalábbis az osztályában – ugyanúgy elrontották a vitatott kérdést. A Telex az idei gimnáziumi felvételi után cikkben hívta fel a figyelmet egy legalábbis félreérthető, de inkább megtévesztő megfogalmazású feladatra. Írásunk után levelek tömkelegét kaptuk, részben további vitatható magyar és matek példákról, de a szülők arról is tájékoztattak bennünket, hogy az Oktatási Hivatal miként reagált a panaszukra.

Mivel a legtöbb levelet a már korábban is ismertetett példára kaptuk, így ennek az utótörténetét részletesebben is követjük, de azért mindenekelőtt bemutatjuk azt is, hogy hol módosult a megoldókulcs.

Hibák mindig vannak, csak javuljanak!

Csak az nem hibázik, aki nem dolgozik – tartja a mondás. Természetesen jó lenne, ha a gyerekek felvételi feladatsorai nem lennének hibásak, félreérthetőek, de ha a hivatal belátja a hibáját és javít, akkor nem marad az emberekben rossz szájíz. Az ilyen korrekcióban nagyon pozitív a félreérthetőség elismerése, az önreflexió. Az idén is több ilyen javítókulcs-módosítás volt. Ezek közül, ami nekünk új hír volt, hogy ez történt például a 8 évfolyamos középiskolák felvételi soránál.

A legutolsó, a 10. példánál mintás csempékről volt szó. A kérdés pedig az volt, hogy hányadik lesz az 5. csempe után a következő olyan csempe, amelyikre igaz lesz az adott állítás.

A jó megoldás a 8. csempe volt, először csak a 8-ast fogadta el a hivatal válaszként. Ám mivel sokan úgy értették a kérdést, hogy az 5. csempe után a 8. csempe a harmadik csempe, belátta a hivatal, hogy az is jól gondolkodott, aki úgy írta le a válaszát, hogy a rajttól a 8-ik csempére igaz az állítás, de az is, aki úgy értette a kérdést, hogy valóban a 8. csempe a jó válasz, de az “5. után” (vagyis, ha az 5. a kiindulás) akkor az a harmadik.

Végül tehát jó megoldás lett a 8. és a 3. is, ami azért bölcs belátás, mert az nem volt reális, hogy aki 3-ast írt, ő az 5. után kérdésre, egy sorban előbbi csempére gondol. A javítókulcsot javították.

A hatodikosok pórul jártak

Nem tágított viszont a hivatal abban a kérdésben, amit vélhetően rengetegen félreértettek. Mi legalábbis sok levelet kaptunk, és tudjuk, hogy az Oktatási Hivatalhoz is sokan fordultak reklamációval, mert a hivataltól kapott egységválaszokat is többen elküldték. A 6 osztályos gimnáziumi felvételi feladatsor 5. feladatának 2. kérdéséről van szó.

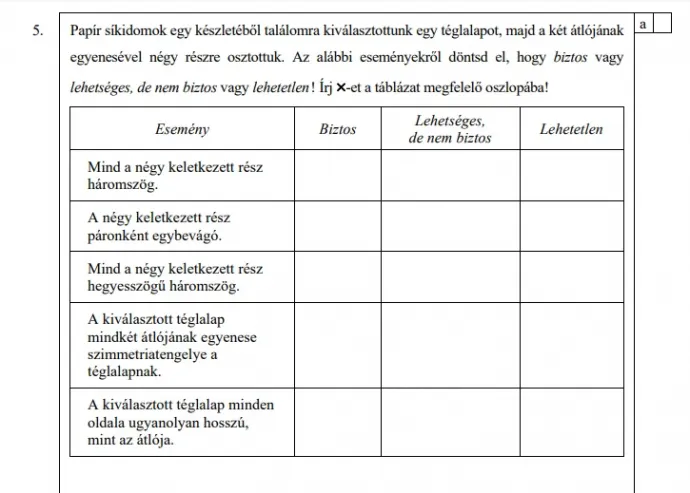
A feladat így szólt: „Papír síkidomok egy készletéből találomra kiválasztottunk egy téglalapot, majd a két átlójának egyenesével négy részre osztottuk. Az alábbi eseményekről döntsd el, hogy

• biztos
• lehetséges, de nem biztos
• lehetetlen!

A 2. állítás így szól: A négy keletkezett rész páronként egybevágó. A javítókulcs szerint ez lehetséges, de nem biztos, de sok diák és tanár is úgy vélekedett, hogy a biztos a jó válasz. Hiszen akár négyzetet, akár más téglalapot is választunk, az átlók behúzása után a szemközti háromszögek egybevágóak lesznek, négyzet esetén pedig mind a négy háromszög egybevágó.

Már első cikkünkben is arra gondoltunk, hogy a feladatíró esetleg arra gondolt, hogy a páronként kifejezés azt jelenti, hogy minden háromszög minden lehetséges másik háromszöggel egybevágó. Vagyis a négyzet megfelel az állításnak, de a nem négyzet téglalapok nem, mert esetükben van olyan háromszögpár, ahol nem teljesül az egybevágóság.

Az persze teljességgel érthetetlen, hogy amennyiben a feladatíró ezt szerette volna kérdezni, minek tette bele a kérdésbe a páronként szót. Miért nem csak annyit írt, hogy “a négy keletkezett rész egybevágó”?

Ráadásul egyáltalán nem elvárható, hogy egy 6. osztályos gyerek a páronként szó esetén ne arra gondoljon, hogy vannak egybevágó párok, hanem arra, hogy minden párosításban minden háromszögpár egybevágó. Ez nemcsak későbbi tananyag, de mint látni fogjuk, még a tananyag sem így használja a kifejezést.

Az Oktatási Hivatal válaszol

Igazi tehetetlenséget azonban akkor érezhettek a gyerekek, a szülők, illetve a felkészítő tanárok, amikor megismerték az Oktatási Hivatal érvelését, amit többen is elküldtek nekünk:

„A négy résznek kell páronként egybevágónak lenni, az azt jelenti, hogy bármely kettő közülük egybevágó. Ha az lett volna a szándékunk, hogy két-két rész legyen egybevágó, akkor azt írtuk volna, hogy a négy rész közül két-két rész páronként egybevágó. Ahogy a paralelogrammánál is két-két szemközti oldala párhuzamos, vagy a deltoidnál két-két szomszédos oldal egyenlő hosszú. A javítási-értékelési útmutatónak megfelelően, a pont nem adható meg más válasz esetében."

Mindez a tanárok tapasztalata szerint azért nagyon zavaró, mert jellemzően a feladatot megértő jó matekosok nem kaptak pontot, azaz még a legjobb tanulók körében is kevés lesz az idén az 50 pontos sor. Különösen zavaró, hogy a gyerekek a háromszögek egybevágóságánál pont abban az értelemben tanulják a páronként kifejezést, hogy „van párja” és nem abban, hogy „mindenki a párja”:

A 9. osztályos tananyagban találhatók a háromszögek egybevágóságának alapesetei. Eszerint két háromszög egybevágó, ha

1. oldalaik hossza páronként egyenlő
2. két-két oldaluk hossza páronként egyenlő, és az ezek által bezárt szögek egyenlők
3. egy-egy oldaluk hossza és a rajtuk fekvő két szögük páronként egyenlő
4. két-két oldaluk hossza páronként egyenlő, és a két-két oldal közül a hosszabbal szemközti szögek egyenlők.

Ha az oldalak hossza páronként egyenlő, akkor egy oldal nem minden másik oldallal egyenlő, hanem van egy párja, amivel egyenlő.

Vagyis a gyerekek pont abban az értelemben tanulják a “páronként” kifejezést, amit a hivatal nem akceptál.

Ennél a feladatnál az lett volna az igazságos döntés, ha a hatodikos szinten nem elvárható értelmezést is, de a korosztálynak megfelelő, józan paraszti ésszel alkalmazott választ is elfogadják, vagyis a biztos és a lehetséges, de nem biztos verziókat is. Na meg persze az lett volna a legjobb, ha eleve nem kerül be a sorba a gyerekeket teljesen értelmetlenül (reméljük nem szándékosan) összezavaró, feleslegesen fontoskodó „páronként” kifejezés.